Inferencia estadística: capacidad de una cucharilla
- Error de la medida
- Recogida de datos
- El Teorema del Límite Central
- La distribución t de Student
- Intervalos de confianza para la media
- Expresar del resultado
No es la primera vez que en este blog utilizamos la excusa más ridícula para repasar ciertos conceptos. En esta ocasión nos planteamos la siguiente pregunta ¿Cuál es la capacidad de una cucharilla de postre, o de una cuchara sopera? Veremos que dar respuesta a eso es tan complicado como queramos hacerlo.
Intentaré explicarlo de manera informal, sin hacer demasiadas cuentas, para que sirva de aclaración de conceptos básicos. Después de todo, quien se quede con ganas de un desarrollo formal (vamos, de ver las cuentas) puede encontrarlo en fácilmente buscando en Google cualquier curso online de estadística.
Error de la medida
La respuesta inmediata es: se coge una cucharilla, y se pesa o se mide una cucharada. Por ejemplo 3.49g. Y ya está, no es tan complicado.
¿Seguro? Vamos a repetirlo: ahora da 4.27g. Sí, distinto. Por varios motivos la cantidad de líquido que porta una cucharilla no es siempre la misma.
Esto es algo habitual en el laboratorio, al medir varias veces una magnitud no obtenemos siempre el mismo resultado. No hablamos de medir la longitud de una mesa o pesar una manzana. La forma de medir esas magnitudes hace que no varíen. Pero hay otras en las que el proceso de medida no es exacto. Por ejemplo ¿cuánto tarda el sonido en llegar de un punto a otro? o ¿cuánto duran 10 oscilaciones de un péndulo? Son magnitudes que en cada medida darán resultados próximos pero diferentes. Esto se debe a varios factores: el aire, nuestros reflejos al iniciar y parar el cronómetro, retardos en la electrónica, etc. Las causas de error son múltiples.
Es importante destacar que no es la magnitud la que varía, porque en la realidad siempre tiene el mismo valor, sino que es el proceso de medición el que debido al error arroja unos resultados distintos cada vez.
En ese caso no podemos decir que la magnitud tiene un valor concreto, podríamos dar una media, o un valor más probable, pero lo más habitual es dar un intervalo de dos valores entre los cuales se espera que esté la magnitud real. Diremos que nuestra medida es más precisa mientras más pequeño sea el intervalo. Por ejemplo diríamos 10±2 si hemos conseguido determinar que la magnitud está entre 8 y 12. En otro experimento podríamos obtener 10±0.1, en ese caso estaría entre 10.1 y 9.9, hemos reducido el rango de valores posibles. Pero nada nos asegura que la medida real sea 10, podría igualmente ser o 10.07 o 9.94. No lo sabemos. Sólo sabemos que no es 150, ni -3. Bueno, más que no es, sólo sabemos que es extremadamente improbable que lo sea. ¿Cómo de poco probable? Más abajo hablaremos de la distribución t de Student y los intervalos de confianza.
Las constantes físicas igualmente tienen error de medida, aunque en muchos textos no se suele indicar. En esta página están recogidas constantes con sus respectivos errores, llamado también incertidumbre.
Recogida de datos
Ahora que sabemos que no basta con hacer una sola medida, vamos a pensar en hacer unas cuantas, y mediante técnicas estadísticas obtendremos el intervalo que decíamos antes.
Es un experimento muy sencillo: tomamos una balanza, y sobre ella colocamos un recipiente ligero. Vamos añadiendo cucharillas de agua y anotamos el peso que indica la balanza. Eso nos daría la capacidad de la cucharilla en gramos, pero si suponemos que la densidad del agua del grifo es 1g/cm³ entonces tenemos la capacidad en ml.
Esta es la hoja de datos que hemos recogido, se trata de dos cucharillas pequeñas y una grande:
Ahora hay que pensar un camino para trabajar con estos datos:
- Por un lado podríamos calcular una regresión lineal, cuya pendiente nos daría la capacidad media. Sin embargo hemos hecho la prueba dos veces, y de alguna manera tendríamos que combinar esas medidas, el cálculo se complica.
- La otra opción es aprovechar que la variable independiente -la X- es incremental: 1 cucharada, 2 cucharadas, 3, 4, 5… así que la capacidad de una cucharada es la diferencia entre cada dos valores consecutivos. Eso es lo que se ve en las columnas Diferencia. Elegimos esta opción.
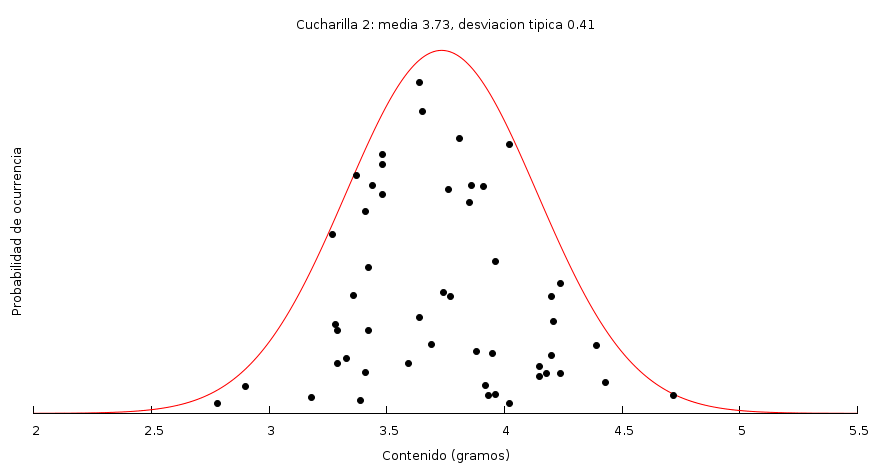
En las columnas Diferencia está la cantidad de agua que contenía cada cucharada… y cada medida es distinta en cada vez. Aún empleando la misma cucharilla, no hay dos cucharadas que contengan exactamente la misma cantidad de líquido. Sabemos que en estos casos en que el error es aleatorio, los valores se distribuyen según la distribución normal o campana de Gauss. Con la muestra de la cucharilla 2 tendría esta forma.
Simplificando, en el eje X está el valor y en el eje Y la probabilidad. Quiere decir esto que los valores más probables se sitúan hacia el centro de la gráfica, pero también pueden existir puntos en los laterales (colas). Pero no prestéis atención a la altura de los puntos, pues esta es aleatoria, lo que nos interesa es la concentración a lo largo del eje horizontal.
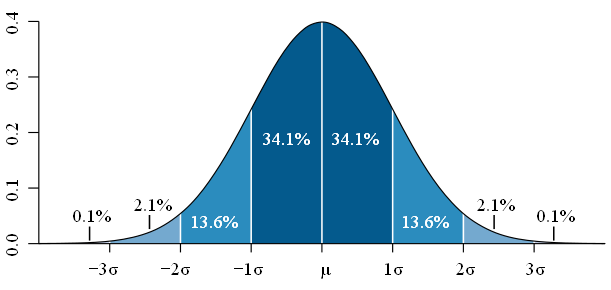
Los valores típicos de la campana se miden en unidades de error, en desviaciones típicas. Así entre la media menos s y la media más s se espera que se sitúen el 68% de las medidas. Entre la media menos 2s y la media +2s se esperan que estén el 95%, etc. Ved esta imagen de la Wikipedia.
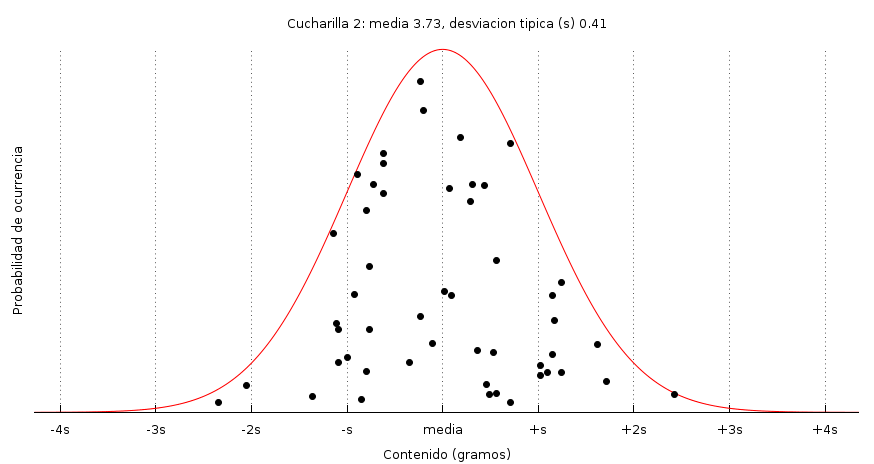
En nuestro caso las medidas se distribuyen de esta manera:
El Teorema del Límite Central
Bien, ya sabemos que si cogiéramos infinitas medidas saldría una campana como la que hemos visto. Pero ahora hay que dar el paso hacia atrás. Es decir, obtener la media global a partir de las medidas, y no tenemos todas la información, ya que no tenemos infinitas medidas, sino sólo 50.
La pregunta que intentaremos responder es: Si tenemos estas 50 medidas ¿cual es la capacidad real? La capacidad real sería la media tras hacer infinitas medidas. Con los datos que tenemos no podemos responder a esa pregunta, porque no hay una respuesta determinada.
Vamos a imaginar que sólo nosotros sabemos esas 50 medidas, (media 3.73, desviación típica 0.41). Alguien quiere medir, y obtiene un subconjunto de nuestras 50, le damos por ejemplo las 25 primeras. Ese alguien calcula la media: 3.56. Pero podríamos haberle dado las 25 últimas: 3.90. O quizá 25 al azar: 3.68. ¿Puede aquel que mide, saber la media de las 50 que teníamos nosotros habiendo medido únicamente 25?
Es obvio que no, no puede. Como mucho puede estimarla. A simple vista, sabe que la media parece estar entre 3 y 4. Pero necesitará hacer uso de algunas técnicas estadísticas para mejorar esa estimación.
Eso mismo nos pasa a nosotros, tenemos 50, pero eso no es más que un subconjunto de las infinitas medidas que podríamos hacer. Así que no sabemos la media exacta. No podríamos decir que es 3.73 porque esa es simplemente la media de nuestra muestra. Si hiciéramos otras 50 medidas, no saldría la misma media.
¿Cuanto saldría?
Es obvio que no lo sabemos, pero podemos suponer que si antes ha salido 3.73, es probable que ronde ese número, y es improbable que saliera muy alejada. Tenemos por tanto otra distribución de probabilidad, que nos dice cómo de probable es obtener una media u otra al hacer un determinado número de medidas sobre una población. Queda saber qué forma tiene esa distribución.
Hay un teorema, que se llama Teorema Central del Límite que dice que si cogemos muchas muestras de una población, y empezamos a calcular sus medias, estas se distribuyen siguiendo una normal. Y da igual que la distribución origen sea normal o no, siempre que el número de muestras sea lo suficientemente grande (mientras más infinito mejor). La desviación estándar de esa distribución es la misma que la de la población original dividido por la raíz cuadrada del número de medidas de la muestra. Para aclaraciones ver este enlace de la Wikipedia o, si entendéis inglés, este vídeo es muy bueno.
Es decir, que si tenemos una muestra con una media de 3.37, y desviación típica 0.41 con 50 datos seguramente venga de una distribución con media también 3.37 y desviación típica 2.9. Pero esto, que es aproximadamente verdad, no es del todo cierto. Porque no sabemos la desviación típica de la población, el 0.41 es tan sólo la de nuestra muestra; la cual, lo mismo que la media variará entre unas muestras y otras.
La distribución t de Student
Así que no pudiendo usar la distribución normal, porque la varianza (que es el cuadrado de la desviación típica) de la población es desconocida, William Sealy Gosset (alias Student) propuso una distribución similar pero que no necesita la varianza de la población total, se apaña con la de la muestra. A cambio es un poco más ancha, porque como no tenemos información precisa hay un aumento de la incertidumbre.
Esta distribución se llama t de Student, o simplemente t. A medida de aumenta el tamaño de la muestra se va pareciendo más a la distribución normal, y con una muestra de más de 25 o 30 medidas el prácticamente ya son idénticas.
Pregunta: ¿Cual es la probabilidad de que teniendo una población total de media X (la que digamos), tomemos una muestra de 50 valores y su media nos dé 3.73?
Respuesta: Por el teorema central del límite que habíamos nombrado antes, sabemos que la distribución de las medias es una distribución normal, independientemente de la forma que tenga la distribución origen.
Pregunta: ¿Cual es la probabilidad de que si tenemos una muestra con media 3.73, esta provenga de una población -normal o no- con media X (la que digamos)?
Respuesta: Pues debería ser también normal, pero como no sabemos la varianza de la población sino sólo la de nuestra muestra, nos tenemos que resignar a usar la menos precisa t de Student.
Intervalos de confianza para la media
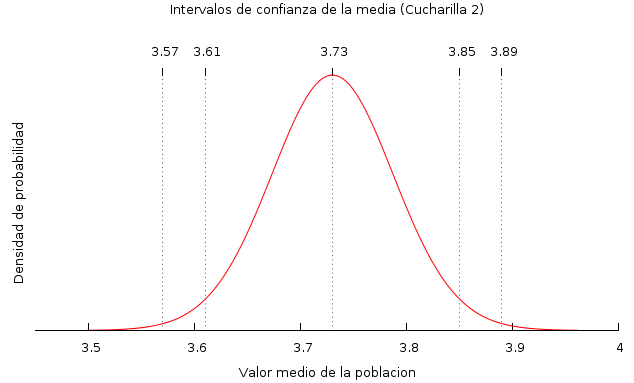
La distribución de t nos dice cual es la probabilidad de que la media de la población origen sea X. Para nuestros datos, teniendo en cuenta la media, el número de medidas y la desviación típica, esta sería la gráfica:
Como vemos, si la media de la muestra es 3.73 lo más probable es que la del total esté en torno a ese valor, simplemente porque no hay motivos para pensar que no sea así. No obstante también podría ser 3.70, o 3.75.
Sin embargo a medida que nos alejamos del valor medio es más improbable que la media de la población vaya a ser esa. Por ejemplo fijaos en el 3.5. Su probabilidad es casi cero. Lo que significa esto es que si la media de 50 valores nos ha salido 3.73 con una desviación típica de 0.41, es muy muy improbable que la muestra venga de una población en la que la media fuera 3.5..
En vista de que no tenemos un valor determinado para la media, sólo podemos indicar el intervalo en que consideramos más probable que esté. Si tomamos el intervalo que va 3.61 a 3.85 tendremos un 95% de probabilidades de que la media real esté contenida en él. Mientras que si cogemos un intervalo más amplio como el que va entre 3.57 y 3.89 la probabilidad sube hasta 99%. Es lo que se denominan intervalos de confianza al 95% o al 99%.
Pregunta:¿Podemos estar seguros de que la media no está, por decir algo, entre 4 y 5?
Respuesta: Podemos estar casi seguros, por ejemplo la probabilidad de que así fuera es de 1 en 80000. Mientras que la del intervalo 5-6 es prácticamente cero.
Pregunta: ¿Pero entonces la media no es 3.73?
Respuesta: ¡No! Es imposible que la capacidad sea un número clavado como 3.73, en la naturaleza no existen esos números tan redondos, los que los redondeamos y aproximamos somos siempre nosotros. La probabilidad de que sea exactamente 3.73 … es justamente cero. Sí, es el valor más probable de todos, pero para nosotros es uno más en el intervalo. De hecho la probabilidad de que la medida real esté comprendida entre 3.73 y 3.74 no llega al 7%. No significa que no pueda ser esa, sino que con los datos que sabemos sólo podríamos asegurarlo con una confianza del 7%.
Expresar del resultado
Siguiendo la convención de usar el intervalo al 95%, diríamos que la capacidad de nuestra cucharilla está entre 3.61ml y 3.85ml (suponiendo la densidad del agua 1 un gramo es igual a un mililitro). O bien, dicho de otra manera, tiene una capacidad de 3.73±0.12ml. Lo que supone un error relativo del 3.2% arriba o abajo.
Aún nos quedan cosas por examinar, pero para una primera aproximación creo que ya está bien. Esas dos preguntas de antes nos conducen directamente a los contrastes de hipótesis, de los que tal vez hablemos en una próxima entrada.