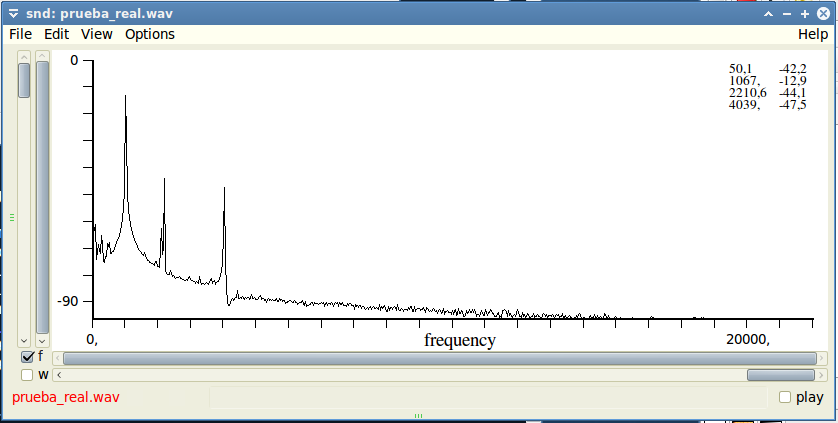
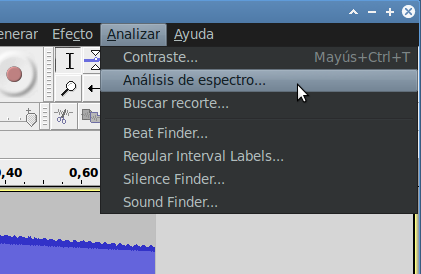
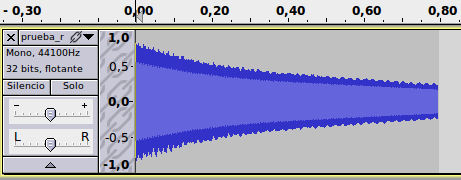
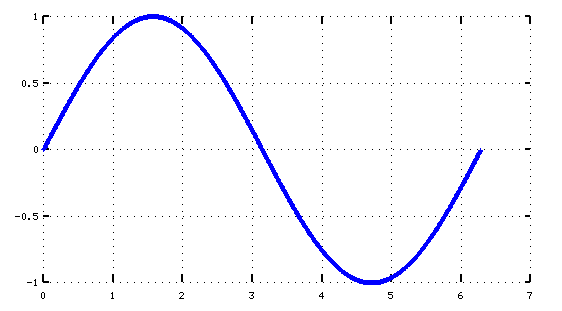
La Transformada de Fourier no es magia
- Correlación
- Análisis de la frecuencia
- Análisis de la amplitud
- Análisis de la fase
- Análisis conjunto
- Fast Fourier Transform
- Caso general
Este no es el típico artículo en plan “¡Ey, no es magia: sólo son matemáticas avanzadas y te da igual porque no vas a entender ni jota!”.
Hace tiempo que quería hablaros de la Transformada de Fourier. Pero no encontraba una forma de presentar el artículo sin que me quedara demasiado matemático. Espero que el enfoque que le voy a dar hoy os sirva para aclarar algunas dudas. Como no quiero entrar en demostraciones muchos puntos los tendré que introducir por las buenas y otros dejarlos a medias. Si algo no os termina de convencer profundizad en el tema, necesitaréis cierto nivel de matemáticas pero comprobaréis que todo está atado y bien atado.
Veréis, los que tenemos formación matemática conocemos la transformada de Fourier como esto:
\[g(\xi ) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} f(x)e^{-i\xi\,x} dx\]mientras que los aficionados al sonido (sobre todo, pero también a la imagen) lo conocen como esto otro:
En ambos casos parece algún tipo de operación, a la que le damos una función y nos saca un gráfico, o nos resuelve una ecuación diferencial. Se habla además del dominio del tiempo y el dominio de la frecuencia, nombres que para el profano no hacen más que acentuar su carácter incomprensible.
Sin embargo lo que hoy os voy a mostrar, si me lo permitís, es que no se trata de ninguna magia negra, o sutiles trucos matemáticos. Sino más bien se parece a un proceso de ensayo y error en el cual -casi de manera tosca- intentamos descubrir el espectro de frecuencias de una señal comparándola con otras. Hablaré sobre todo de sonido, por no complicar las cosas; aunque de aquí a unas semanas veremos un uso de esta operación en dos dimensiones.
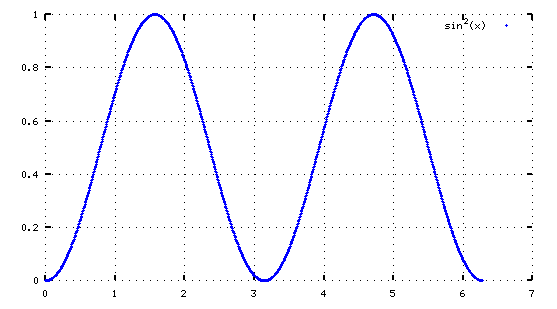
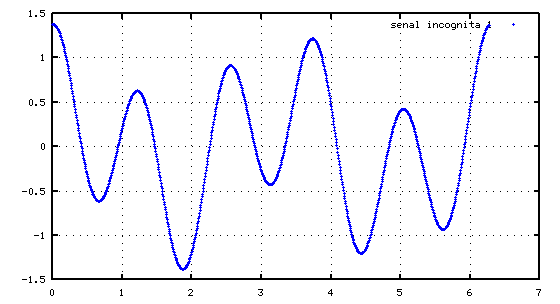
Tenemos una señal, por ejemplo la de arriba. Escuchadla. Es un sonido suave, pero ¿de qué frecuencia? ¿Es sólo de una frecuencia pura o es una mezcla de varias?
Correlación
Antes de dar respuesta a la pregunta anterior, hay que familiarizarse con otro proceso: la correlación. La correlación, que es la base de todo este artículo, consiste en comparar dos señales y ver cómo son de similares. En la Wikipedia encontraréis la definición formal, pero hoy nosotros vamos a usarla a nuestra manera.
En primer lugar definimos un intervalo. Que será un vector de N puntos igualmente espaciados. Por ejemplo tomaremos el intervalo de 0 a 2π. ¿Por qué? Pues porque como vamos a trabajar con senos y cosenos parece una elección apropiada. Claro que no es la única opción válida. Y dentro de ese intervalo evaluamos la función en 1000 puntos (1000 samples).
npuntos = 1000;
inicio = 0;
fin = 2*pi;
% Ancho de cada punto.
bw = (fin-inicio)/npuntos;
% El intervalo es un abierto:
% quitar el último punto.
x = [inicio:bw:fin-bw];
x es nuestro intervalo. Ahora definimos una función en ese intervalo, por ejemplo el seno de x:
Ahora vamos a multiplicar \(\sin(x)\) por \(\sin(kx)\) . Iremos variando k. Cuando k es 1, en realidad tenemos \(\sin(x)\times\sin(x)\) . Que es el seno al cuadrado, y todos los valores son cero o positivos.
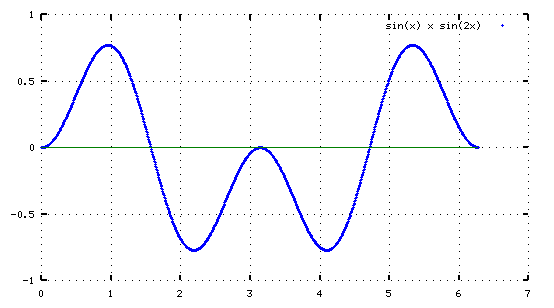
Pero veamos qué pasa cuando lo multiplicamos por un k distinto de 1, por ejemplo 2:
La función es simétrica (antisimétrica si multiplicáramos por el coseno). El resultado llama mucho más la atención si cogemos los valores de cada punto en el intervalo y los sumamos. Porque en el caso del cuadrado, como todos los valores eran positivos su suma es positiva. Pero ahora al ser simétrica el resultado es cero:
octave:26> sum(sin(x).*sin(1*x))
ans = 500
octave:27> sum(sin(x).*sin(2*x))
ans = 0
octave:28> sum(sin(x).*sin(3*x))
ans = 0
octave:29> sum(sin(x).*sin(4*x))
ans = 0
Lo más curioso es que si tenemos \(\sin(ax)\times\sin(bx)\) casi siempre dará cero. Con una excepción: sólo cuando \(a=b\) nos dará algún valor distinto. Mayor cuanto más puntos tenga el intervalo. Ahora probamos con una frecuencia arbitraria, por ejemplo el 6:
octave:30> sum(sin(6*x).*sin(4*x))
ans = 0
octave:31> sum(sin(6*x).*sin(5*x))
ans = 0
octave:32> sum(sin(6*x).*sin(6*x))
ans = 500
octave:33> sum(sin(6*x).*sin(7*x))
ans = 0
Y no solo eso, lo mismo ocurre si pruebo a multiplicar por el coseno: aún con la misma frecuencia sale cero.
octave:35> sum(sin(6*x).*cos(6*x))
ans = 0
octave:36> sum(sin(6*x).*sin(6*x))
ans = 500
La correlación es un indicador de cuánto se parece una señal a otra. Lo que ocurre con las funciones trigonométricas es un caso especial. Se dice que dos señales son perpendiculares (ortogonales) cuando su correlación es cero. De igual manera que se dice que dos vectores son ortogonales cuando su producto escalar vale cero.
Ahora viene una nota de álgebra, si no os interesa el trasfondo matemático del asunto saltaos este párrafo. También al igual que con los vectores, si tenemos un conjunto de funciones en este caso ortogonales podemos formar una base y expresar las componentes de cualquier función en esa base. Hemos visto que las funciones seno y coseno forman una base ortogonal en un espacio de dimensión infinita (porque hay infinitas frecuencias distintas) -un espacio de Hilbert-. Ese es el dominio de la frecuencia, por contraposición al dominio del tiempo. Los componentes de la función expresados en la base que hemos encontrado son los coeficientes de Fourier. Aunque la correlación no es exactamente lo mismo que el producto escalar de dos funciones, para nuestro caso sirva la comparación.
En la dspguide encontraréis información ampliada de este tema y muchos otros. Recomiendo que la leais si os interesa el DSP.
Análisis de la frecuencia
Todavía no vamos a hablar de Hercios, solamente llamamos frecuencia al número que va multiplicando el argumento del seno o coseno para entendernos. Más adelante ya veremos con qué se corresponde.
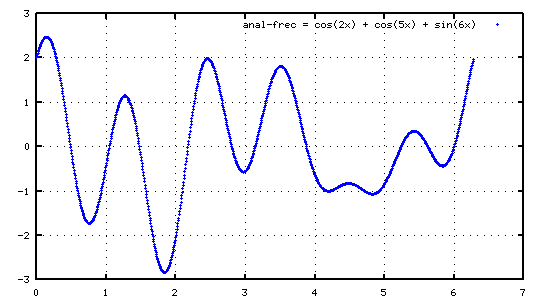
Ya hemos visto lo que pasa cuando “comparamos” (correlamos) funciones de una sola frecuencia, sinusoidales puras. Pues vamos a componer una función sumando frecuencias puras y a ver si también podemos hacer el mismo análisis que hemos hecho antes. Cogemos nuestra onda de muestra, por ejemplo una composición de cosenos y senos con las frecuencias 2, 5 y 6:
\[anal\_frec = \cos 2x +\cos 5x +\sin 6x\]Lo llamamos anal_frec para que sea más fácil de leer. Esto es lo que pasa cuando multiplicamos y sumamos con las diferentes frecuencias. Probamos sólo hasta la 9:
Usando el coseno:
sum(anal_frec.*cos(1*x)) = 0
sum(anal_frec.*cos(2*x)) = 500
sum(anal_frec.*cos(3*x)) = 0
sum(anal_frec.*cos(4*x)) = 0
sum(anal_frec.*cos(5*x)) = 500
sum(anal_frec.*cos(6*x)) = 0
sum(anal_frec.*cos(7*x)) = 0
sum(anal_frec.*cos(8*x)) = 0
sum(anal_frec.*cos(9*x)) = 0
Usando el seno:
sum(anal_frec.*sin(1*x)) = 0
sum(anal_frec.*sin(2*x)) = 0
sum(anal_frec.*sin(3*x)) = 0
sum(anal_frec.*sin(4*x)) = 0
sum(anal_frec.*sin(5*x)) = 0
sum(anal_frec.*sin(6*x)) = 500
sum(anal_frec.*sin(7*x)) = 0
sum(anal_frec.*sin(8*x)) = 0
sum(anal_frec.*sin(9*x)) = 0
Ya veis cómo se identifican perfectamente las frecuencias que componen la señal. ¿Cuanto menos es curioso, no?
Análisis de la amplitud
Ya hemos comprobado que en una suma de varias frecuencias el resultado es cero salvo para las frecuencias que componen la onda. ¿Y cuando no vale cero, cuánto vale? Pues es independiente de la frecuencia, y en nuestro dominio de 0 a 2π vale justo la mitad de los puntos del intervalo. Aunque puede ser distinto en otras definiciones de la función. Si había mil puntos, el resultado es 500. Como digo independientemente de la frecuencia, y ya sea para el seno o para el coseno, ved:
sum(sin(3*x).*sin(3*x)) = 500
sum(sin(7*x).*sin(7*x)) = 500
sum(cos(4*x).*cos(4*x)) = 500
sum(cos(9*x).*cos(9*x)) = 500
Un resultado más práctico sería dividir por ese valor máximo. Así nos dará 1 cuando las funciones son iguales y 0 cuando son completamente diferentes. Y siempre dará el mismo valor cojamos los puntos que cojamos. A esta operación se le llama normalización.
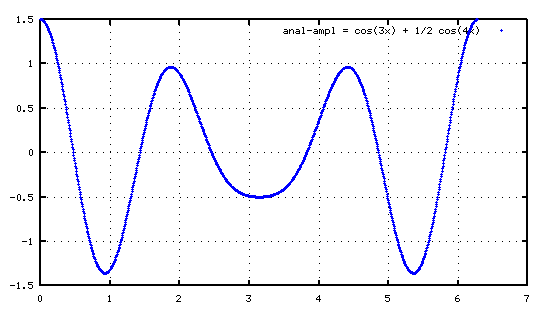
Y digo que es un valor más práctico porque mirad lo que pasa cuando sumo funciones de diferentes amplitudes:
\[anal\_ampl = 1\cos 3x + \frac{1}{2} \cos 4x\]Ahora hago el mismo análisis que antes, hasta el 5 para abreviar:
sum(anal_ampl.*cos(1*x))/500 = 0
sum(anal_ampl.*cos(2*x))/500 = 0
sum(anal_ampl.*cos(3*x))/500 = 1
sum(anal_ampl.*cos(4*x))/500 = 1/2
sum(anal_ampl.*cos(5*x))/500 = 0
El resultado es 1 para la frecuencia 3, porque para eso hemos dividido. Mientras que para la frecuencia 4 sólo es 0.5, que justamente es la amplitud que le habíamos puesto a esa frecuencia.
Hasta aquí ya podemos analizar una muestra y saber de qué frecuencias de compone y en qué proporción.
Análisis de la fase
¿Y qué pasa si nuestra sinusoide no empieza en 0? Por ejemplo si tenemos esto:
\[anal\_fase = \cos (2x + \frac{1}{2})\]Si lo analizamos con el coseno ya no nos da 1:
sum(anal_fase.*cos(2*x))/500 = 0.87758
Y más extraño aún, cuando le aplicamos el seno obtenemos un valor negativo:
sum(anal_fase.*sin(2*x))/500 = -0.47943
El 1/2 es la fase inicial, que va desde \(-{\pi \over 2}\) a \(+{\pi \over 2}\) . El que los resultados no sean 0 y 1 lo que nos dice es que la onda no viene ni de un seno ni de un coseno. Sino que es una mezcla del seno y coseno.
Lo que siempre siempre va a ocurrir es que la suma de los cuadrados es igual a la amplitud al cuadrado. En este caso es 1:
octave:83> 0.87758^2 + (-0.47943)^2
ans = 1.00000
y de ahí, es suficiente tomar la raíz cuadrada para saber la amplitud.
El ángulo, la fase inicial, la podemos obtener a partir de la tangente. O más bien de su inversa, la arcotangente.
\[\phi = \arctan\left(\frac{-sin}{cos}\right)\]El signo negativo del seno es por convenio. Para que el signo del ángulo coincida con el signo que lleva la fase en el argumento del seno. Realmente hay una justificación de más peso que tiene que ver con la definición de correlación, pero la voy a obviar.
El asunto para el ángulo ya está resuelto.
Hay un “truco” muy práctico en matemáticas: cuando queremos llevar dos cantidades relacionadas al mismo tiempo usamos números complejos. Y en este caso vamos a usar la parte real para llevar la correlación con el coseno y la parte imaginaria para llevar la correlación con el seno. ¿Y por qué no al revés? Pues para que sea consistente con la relación de Euler:
\[e^{i x} = \cos x + i\,\mbox{sen}\,x\]Ahora es fácil continuar: la amplitud será el módulo del número complejo y la fase su argumento. Y tiene todo el sentido lo de la arcotangente ¿verdad? Así es como funciona con el ejemplo de antes:
octave:84> anal_fase = cos(2*x+0.5);
octave:86> real = sum(anal_fase.*cos(2*x))/500;
octave:87> imag = sum(anal_fase.*sin(2*x))/500;
octave:88> modulo = real^2+imag^2
modulo = 1
octave:89> argumento = atan(-imag/real)
argumento = 0.50000
Bien, para una señal ya sabemos decir qué frecuencias la componen, en qué proporción y qué fase inicial tiene cada una.
Vamos a meter estos cálculos en una función para tenerlos bien a mano y le llamamos por ejemplo correla.
function [amplitud, fase, real, imag] = correla(frecuencia, senal, intervalo)
% Asumimos que tanto senal como intervalo son un vectores fila de igual tamaño.
norm = numel(intervalo)/2;
% Calculamos parte real e imaginaria.
real = sum(senal.*cos(frecuencia*intervalo))/norm;
imag = sum(senal.*sin(frecuencia*intervalo))/norm;
% Al invertir la parte imaginaria elegimos que la fase
% tenga el mismo signo que en el coseno. Además así coincide
% con la que da la FFT.
imag = -imag;
% Calculamos coordenadas polares.
amplitud = sqrt(real^2+imag^2);
fase = atan(imag / real);
end
Recibe como argumentos la frecuencia con la que queremos probar, la señal incógnita y el dominio. Y nos devolverá el resultado tanto en coordenadas cartesianas (parte real e imaginaria) como en polares (módulo y argumento).
Análisis conjunto
Es hora de analizar una señal de prueba desconocida:
Lo primero en que hay que fijarse es en las amplitudes. No tendremos en cuenta los valores por debajo de un límite, y los consideraremos 0. Y después la fase: porque la fase no nos importa nada si la amplitud es muy pequeña. De hecho la fase es un cociente, y cuando el divisor se hace cada vez más pequeño es propensa a ir dando tumbos.
Tomamos nuestra función y vamos probando con cada frecuencia. A mano es un tanto repetitivo así que sólo probaremos desde el 1 hasta el 5 e iremos viendo qué resultados nos da correla:
octave:114> [ampl, fase] = correla(1,senal_incognita_1,x)
ampl = 0
fase = 1427/4840
octave:115> [ampl, fase] = correla(2,senal_incognita_1,x)
ampl = 1/2
fase = -333/1000
octave:116> [ampl, fase] = correla(3,senal_incognita_1,x)
ampl = 0
fase = 753/80815
octave:117> [ampl, fase] = correla(4,senal_incognita_1,x)
ampl = 0
fase = -349/5059
octave:118> [ampl, fase] = correla(5,senal_incognita_1,x)
ampl = 9/10
fase = 0
Las frecuencias con amplitud distinta de 0 son 2 y 5, la frecuencia 2 tiene 1/2 de amplitud y su fase inicial es aproximadamente -1/3. La amplitud de la frecuencia 5 es 9/10 y no tiene fase inicial, es 0. Comparemos el resultado con la primera señal incógnita, que es:
senal_incognita_1 = 0.5*cos(2*x-0.333) + 0.9*cos(5*x);
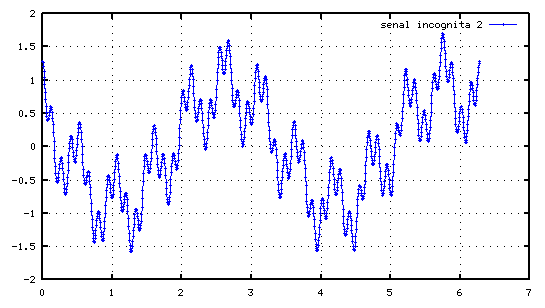
No está nada mal. Vamos con la segunda señal incógnita:
Esas ondulaciones parecen de una frecuencia mucho más alta que 5. Así que si nos ponemos a hacerlo a mano nos vamos a aburrir. Mejor lo metemos dentro de un bucle y hacemos que el programa pruebe automáticamente las frecuencias desde 1 hasta, por ejemplo 50 y que escriba por pantalla únicamente las amplitudes que superen un valor, digamos 0.001:
function analiza_correla(senal,intervalo)
% Vamos correlando la señal con frecuencias desde 1 a 50
for i = [1:50]
[ampl,fase] = correla(i, senal, intervalo);
% Sólo escribir las que superen cierta amplitud
if (ampl > 0.001)
printf("Frec: %d -> Ampl: %4.3f, Fase: %4.3f\n", i, ampl, fase)
endif
end
end
El resultado es:
octave:119> analiza_correla(senal_incognita_2,x)
Frec: 2 -> Ampl: 0.900, Fase: 1.000
Frec: 12 -> Ampl: 0.500, Fase: -0.000
Frec: 47 -> Ampl: 0.300, Fase: 0.000
Efectivamente, la definición de senal_incognita_2 era:
senal_incognita_2 = 0.9*cos(2*x+1) + 0.5*cos(12*x) + 0.3*cos(47*x);
La función analiza_correla, esa que nos da las frecuencias y las fases de cualquier señal, no es sino una versión casera de nuestra transformada de Fourier.
Fast Fourier Transform
Lo que hemos hecho hasta ahora es lo que se llama una DFT, una transformada discreta de Fourier. La FFT o transformada rápida de Fourier es un algoritmo para calcular lo mismo pero de manera mucho más rápida. Gracias a él, muchos programas reproductores nos muestran el espectro en tiempo real según va sonando la canción.
En octave la función FFT recibe una forma de onda y devuelve un vector de números complejos de todas las frecuencias posibles (es un poco más, pero de momento nos quedamos con esto). El primer elemento del resultado corresponde con la frecuencia 0, la componente continua de la señal. Lo hemos obviado antes y lo vamos a omitir ahora porque es un caso especial. El segundo elemento es la frecuencia 1, el tercero la 2, y así.
Montamos un bucle similar al que hicimos con correla; salvo que en lugar de calcular la FFT frecuencia a frecuencia, calculamos todo y luego el bucle actúa sobre el vector de resultados:
function analiza_fft(senal)
% Calculamos la FFT de la senal de entrada
% Nos devolverá coordenadas cartesianas, pasamos a polares.
real_imag = fft(senal);
ampl = abs(real_imag);
fase = arg(real_imag);
% Dividimos para normalizar, en la función correla ya lo habíamos
% tenido en cuenta pero FFT no lo preve.
norm = numel(senal)/2;
ampl = ampl / norm;
% Calculamos las frecuencias del 0 al 50
% El primer elemento de la matriz es 1.
for i = [1:50]
% Sólo escribir las que superen cierta amplitud
if (ampl(i+1) > 0.001)
printf("Frec: %d -> Ampl: %4.3f, Fase: %4.3f\n", i, ampl(i+1), fase(i+1))
endif
end
end
Y este es el resultado que da al aplicarlo sobre la señal incógnita 2:
octave:120> analiza_fft(senal_incognita_2)
Frec: 2 -> Ampl: 0.900, Fase: 1.000
Frec: 12 -> Ampl: 0.500, Fase: 0.000
Frec: 47 -> Ampl: 0.300, Fase: 0.000
El mismo exactamente que nuestra transformada casera. Como debe ser.
Caso general
Bueno, ahora que ya sabemos algo mejor lo que hace la transformada de Fourier vamos a aplicarla a un caso general. Retomemos el archivo de audio del principio y a ver si somos capaces de descomponerlo.
Se trata de un wav, grabado a 44100Hz:
> file prueba_real.wav
prueba_real.wav: RIFF (little-endian) data, WAVE audio, Microsoft PCM, 16 bit, mono 44100 Hz
Cargamos el fichero en Octave:
octave:123> senal = wavread ("prueba_real.wav");
Veamos el tamaño:
octave:129> size(senal)
ans =
35142 1
Tiene 35142 samples, si tuviera 44100 duraría exactamente un segundo. En este caso dura 0.796 segundos simplemente dividiendo.
Vamos a pasar de las funciones que hemos hecho y vamos a ir al grano ¿cómo se usa la función FFT?
Calculamos la FFT de nuestra señal y la dividimos entre la mitad del número de puntos en el intervalo. Ojo que este intervalo no va de 0 a 2π, sobre el valor de normalización podríamos hablar más, pero después de todo no es más que un factor de escala.
octave:151> fourier = fft(senal)/17571;
octave:152> size (fourier)
ans =
35142 1
Ya vemos que nos devuelve un vector del mismo número de elementos que el que le pasamos. ¿Qué contiene el resultado?
- El primer elemento. El elemento 0 (aunque aquí es 1 porque el índice de las matrices en octave comienza por 1) es la frecuencia 0. Esto es, la componente continua. Aquí va a ser casi siempre muy pequeña, prácticamente 0 porque las tarjetas de sonido incorporan un condensador para eliminar la continua. Cualquier valor que aparezca se deberá al offset de fábrica del conversor ADC que incorpore la tarjeta. Como curiosidad siempre es real, y el valor que sale es el doble.
- Los elementos del 1 a la mitad del intervalo, en este caso del 2 al 17571 son complejos como los que hemos visto ya. Su módulo indica la amplitud y su argumento la fase de la frecuencia. El elemento 2 corresponde a la frecuencia más baja y el 17571 a la más alta. ¿Cual es la frecuencia más alta? Pues es precisamente la mitad de la de muestreo. Ese resultado se llama Teorema de Nyquist-Shannon. Como el archivo se grabó a 44100 muestras por segundo, la mayor frecuencia que se pudo registrar es de 22050Hz (que ya está por encima del rango audible, por eso los CD se graban a 44100Hz).
- El elemento 17572, justo en el punto medio, nos aparece porque tenemos un número par de puntos. Quitando el primer elemento que es el 0, queda un número impar de puntos. Es también real siempre.
- Los elementos del 17573 en adelante, no aportan más información de la que ya tenemos, pues no son más que los complejos conjugados de los elementos anteriores (del 2 al 17571) a modo de espejo.
Así que para nuestro análisis nos quedamos con los elementos que van desde el 1 al 17571 y descartamos el resto:
fourier = fourier(1:17571)
De esos, el 1 es la frecuencia 0Hz y el 17571 corresponde a 22050Hz. Aquí es muy importante que notéis que la frecuencia máxima sólo depende de la velocidad de muestreo, mientras que la FFT va a devolver más o menos valores según el tamaño de la muestra que le pasemos. Por eso al analizar muestras muy breves no tenemos precisión en la frecuencia (salen muy pocos puntos), y para tener precisión en la frecuencia necesitamos muestras más largas, con lo que perdemos precisión en el tiempo. ¿No os suena a un principio de incertidumbre? Justo, es eso mismo.
Las frecuencias hemos dicho que van del 0 al 22050, en un intervalo que tiene 17571 puntos:
% -- Intervalo --
npuntos = 17571;
inicio = 0;
fin = 22050;
% -- Fin de los datos --
% Ancho de cada punto.
bw = (fin-inicio)/npuntos;
% El intervalo empieza en 0:
% quitar el último punto.
frecs = [inicio:bw:fin-bw];
Como a priori no tenemos idea de por donde andan las amplitudes, no tiene sentido fijar un umbral mínimo. Así que lo mejor será hacer un gráfico inicialmente para tener una idea. Aquí no nos interesan las fases, sólo las amplitudes.
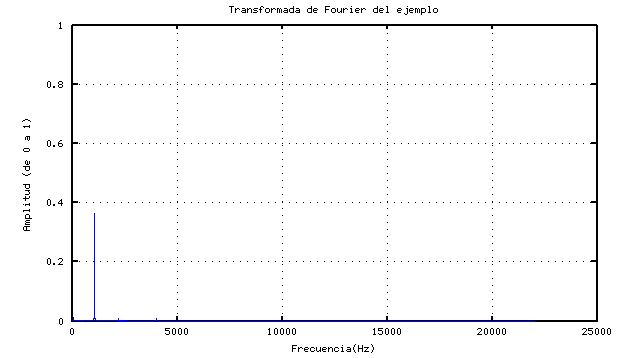
plot(frecs, abs(fourier))
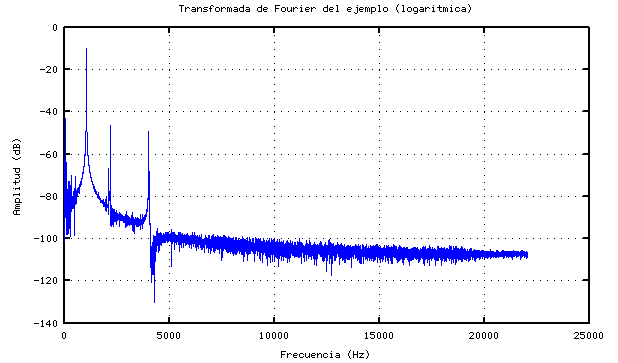
La verdad es que así no se ve mucho. Por eso las amplitudes suelen expresarse en unidades logarítmicas: el Belio, o más usado el decibelio. Así que vamos a tomar logaritmos para ver si conseguimos recortar un poco los picos y ver también la parte baja:
Eso está mejor. Ahí vemos el espectro de frecuencias de la señal de entrada. En particular destacan tres, pero en ese gráfico es difícil decir cuales. Veamos qué frecuencias superan los -55dB en ese gráfico.
Primero obtenemos un vector con las amplitudes en decibelios.
decibelios = 10*log(abs(fourier));
Y seleccionamos de tales amplitudes aquellas que superen los -55dB:
picos = find(decibelios > -55);
Y sabiendo las posiciones de los picos, listamos las frecuencias y las amplitudes correspondientes:
octave:231> [frecs(picos)' decibelios(picos)]
ans =
50.196 -43.140
...
1062.908 -31.894
1064.163 -28.219
1065.417 -22.614
1066.672 -10.076 *
1067.927 -17.641
1069.182 -25.794
1070.437 -30.263
...
2209.894 -48.728
2211.149 -46.431 *
2212.404 -53.628
...
4038.296 -50.119
4039.551 -49.515 *
Y ya lo tenemos, las frecuencias que componen el tono son 50Hz (probablemente zumbido de alterna captado por el micrófono), principalmente 1066Hz (el pico es de -10dB), y en menor proporción también destacan 2211Hz y 4039Hz. Ni que decir tiene que hay programas que identifican los picos automáticamente, pero siempre es recomendable hacer este tipo de ejercicios a mano al menos una vez.
Por ejemplo snd tiene múltiples opciones de análisis. El resultado no puede ser idéntico por algunos detalles del proceso en los que no voy a entrar, pero sí es muy parecido tanto en las frecuencias de los picos como en su valor. Esa es precisamente la imagen con la que abríamos este artículo:
También supongo que habréis visto en sitios que en lugar de hacerlo con el módulo del resultado lo hacen con el cuadrado. Se hace cuando nos interesa más la potencia que la amplitud, pues esta varía con el cuadrado de la amplitud. No importa, como hemos tomado logaritmos calcular el cuadrado no es más que multiplicar por dos; al fin y al cabo un simple cambio de escala, pero el resultado es el mismo. Lo mismo que ocurría con la normalización. La diferencia sólo se nota si vamos a usar los resultados numéricos en cálculos posteriores.