Estadística de los exámenes tipo test
- Nota esperada
- Compensar el resultado
- ¿Y qué pasa con los valores negativos?
- Significación estadística
- Para terminar
La semana pasada hice un examen tipo test. Eran 150 preguntas y pedían, para aprobar, el 70%. La pregunta es ¿ese 70% tiene su justificación matemática o es más bien un limite arbitrario? Vamos a hablar de cómo interviene el azar al responder preguntas y de las diferentes formas de compensarlo.
Nota esperada
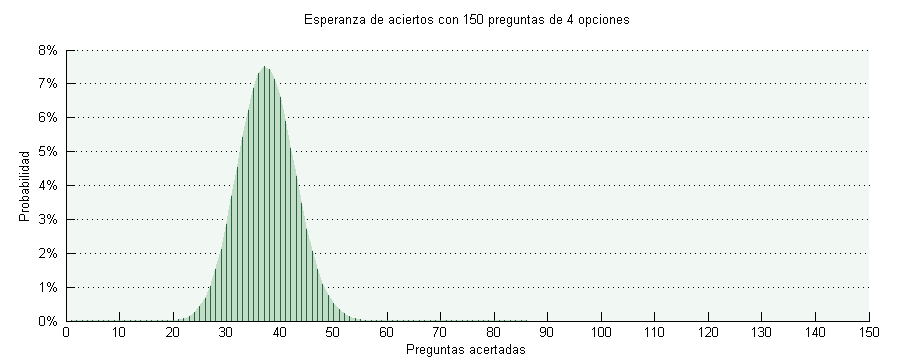
Comenzaremos con el examen que os digo, 150 preguntas de 4 opciones. Alguna había de respuesta múltiple y de verdadero/falso, pero las vamos a obviar. Si hay cuatro opciones y sólo una es la correcta, no se te escapa que haciéndolo a boleo acertaremos una de cada cuatro preguntas, que son 37. Eso es un 25%. Pero vamos a profundizar un poco más, no siempre que lo hagamos vamos a acertar 37 preguntas. La probabilidad de acertar un número determinado de preguntas viene dada por la distribución de binomial con parámetro P igual a 0.25.
Como siempre, pinchad en las imágenes para verlas ampliadas. Lo más probable, sí, es que acertemos 37. Pero sólo pasará entre 7 y 8 veces de cada cien que hagamos el examen. Acertar 30 o 40 no es improbable. Acertar 60 ya empieza a ser más difícil, y las 150 prácticamente imposible. Para que os hagáis una idea, junto al gráfico de arriba, la probabilidad de acertar X preguntas es:
| 37: | 1 de cada 13 veces |
| 50: | 1 de cada 200 veces |
| 60: | 1 de cada 50.000 veces |
| 100: | 1 de cada 1 y 26 ceros detrás |
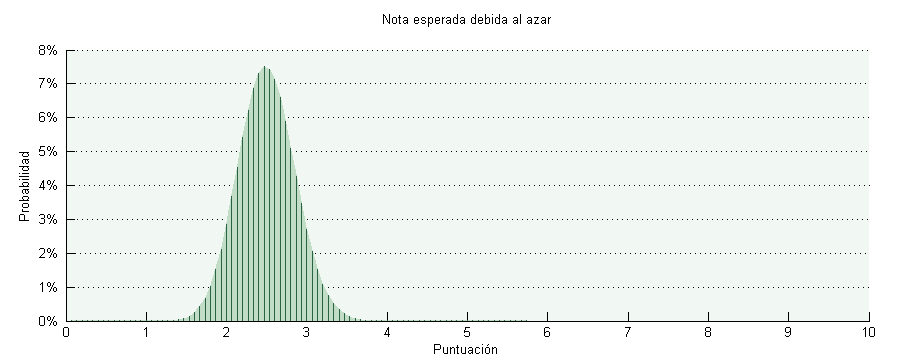
Si no acertar ninguna representar lo que sería un 0 patatero, y acertarlas todas el 10, esta es la nota esperada por azar, según lo que hemos visto.
No es más que un cambio de escala en el eje x, la forma sigue siendo la misma. Lo más probable, si no se sabe nada de nada, es sacar entre un 1.5 y un 3.5.
Compensar el resultado
Ahora bien, normalmente dejamos el 0 para el que no sabe nada y el 10 para el que se lo sabe todo. Y aquí resulta que el que no sabe nada sacará un 2 y medio. Pues lo que se hace es compensar esa diferencia. Hay dos métodos que en esencia son lo mismo:
Descontar preguntas falladas: Es decir, que cada pregunta que se falle descuente una cantidad. Para que si se hace a boleo, las acertadas se cancelen con las falladas y el total se anule. ¿Cuánto hay que restar? Pues si hemos visto que lo más fácil es que acierten 37, dividimos esas 37 entre las fallidas que son 150 menos 37, o sea 113. 37 entre 113 da aproximadamente 0.33 puntos, esto es un tercio de la pregunta.
Repito: en un test de 4 opciones, da igual cuántas preguntas sean, cada pregunta mal debe restar un tercio de punto. Si resta 0.25 está mal diseñado. Si resta una pregunta entera por cada pregunta mal, el autor merece que lo cuelguen por los pulgares del palo mayor.
En general, la fórmula para saber cuanto hay que descontar por cada fallo es:
\[D={1 \over (N-1)}\]donde N es el número de preguntas. Así sólo en el caso de un test verdadero/falso, que tan sólo tiene dos opciones por pregunta descontaríamos una pregunta por cada fallo.
Es un error común dividir entre el número de opciones y descontar esa cantidad. Digamos 0.25 en uno de cuatro opciones, o 0.5 en uno de verdadero/falso. Intuitivamente nos olvidamos de que la pregunta que está mal no puntúa, no sólo descuenta sino que no ha contado. Por eso hay que dividir el total entre N-1 y no entre N. Es más benévolo, eso sí porque resta menos de lo que debe, pero es por otro lado injusto.
Exigir más aciertos. Es más elegante, o por lo menos a mi me lo parece, subir el mínimo para aprobar que andar restando puntos. De ahí que en mi examen del otro día me pidieran un 70%. Veamos, si lo esperado es que acertara 37 preguntas, podríamos fijar ahí el 0 y contar sólo cuántas preguntas acertadas por encima del umbral aleatorio hay.
Esto sería como asignarle un 0 a 37 preguntas acertadas y un 10 a las 150. Un sistema de ecuaciones sencillo:
37a + b = 0
150a + b = 10
De donde
a = 0.088
b = -3.275
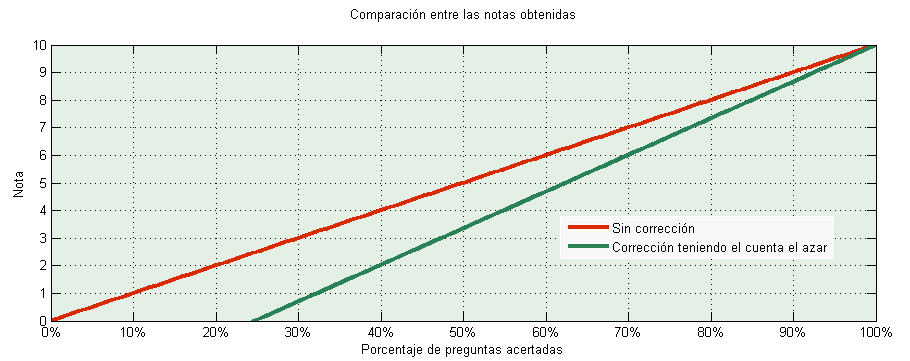
Ambos métodos son el mismo. Y gráficamente se hace evidente:
Si no compensamos el efecto del azar (línea roja) cuando sólo acertábamos el 25% y fallábamos el resto, obtendríamos un 2.5 sobre 10. En cambio tras la corrección (línea verde), con ambos métodos obtendríamos un cero.
Digamos que se aprueba con un 5. En el primer caso para aprobar nos bastaría con el 50%. Sin embargo ahora necesitamos aproximadamente un 60%. En mi caso no exigían el 60% sino un 70%, que es más de lo que nos dicen las matemáticas. Diríamos que para aprobar hace falta un 6. Si bien muchas de las preguntas están disponibles en Internet, por lo que es normal que pidan algo más del 5 pelado para pasar.
Obtener una calificación del 80% no es sacar un 8, sino poco más de un 7.
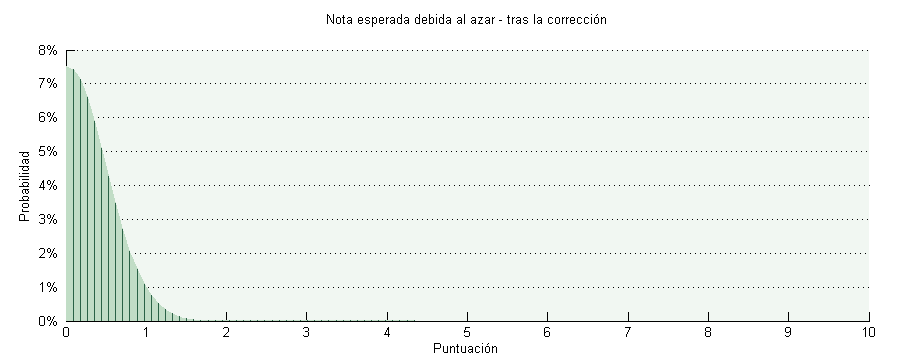
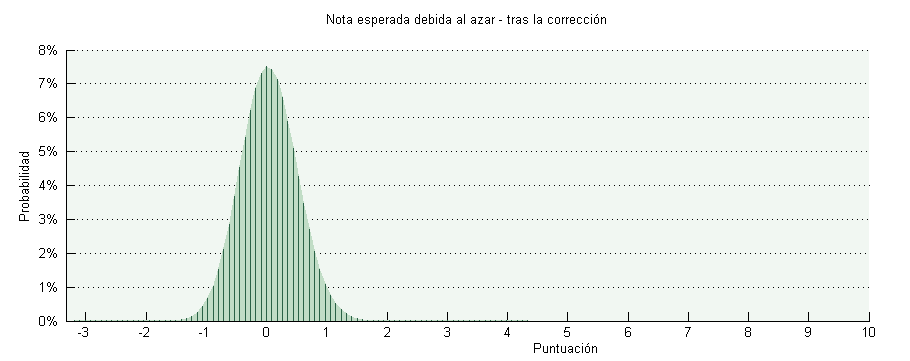
Volviendo al gráfico de la binomial con el que empezamos, lo que hemos hecho es meramente un desplazamiento de todo el gráfico hacia la izquierda:
Ahora lo más probable, si se hace a boleo es sacar entre un 0 y un 1 y algo. Sacar un 2 es improbable y para aprobar hay que saber (o tener mucha, mucha suerte, volveremos sobre este punto más tarde).
¿Y qué pasa con los valores negativos?
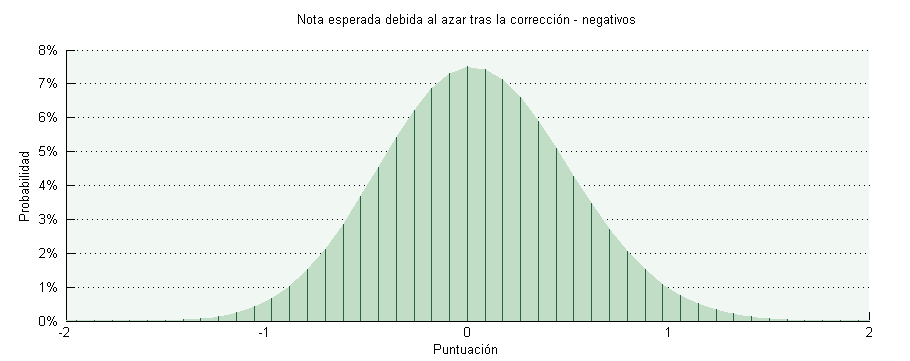
Creo que todos sabemos de alguien que sacó nota negativa en un examen. Mirad la nota esperada tras la compensación:
La misma probabilidad hay de sacar un 1 que un -1. Asimismo al igual que para sacar un 2 o un 3 hay que saber algo, para sacar un -2 o un -3 hay que no saber algo -o fallar adrede, claro-. No hablo de desconocer un tema, sino de tener un conocimiento negativo. Un ejemplo divertido, ved cómo empieza esta conferencia de TED: Hans Rosling shows the best stats you’ve ever seen.
¿Cuánto es el mínimo que se puede sacar? En este examen de 4 opciones, si está bien diseñado, cada pregunta restaría un tercio de punto. Luego lo mínimo que se puede sacar, fallando todas, es un -3.33. En un examen de dos opciones, donde cada fallo resta un punto entero, se puede llegar a sacar un -10, claro que sería tan improbable como sacar un 10. Para eso habría que “menos saber”.
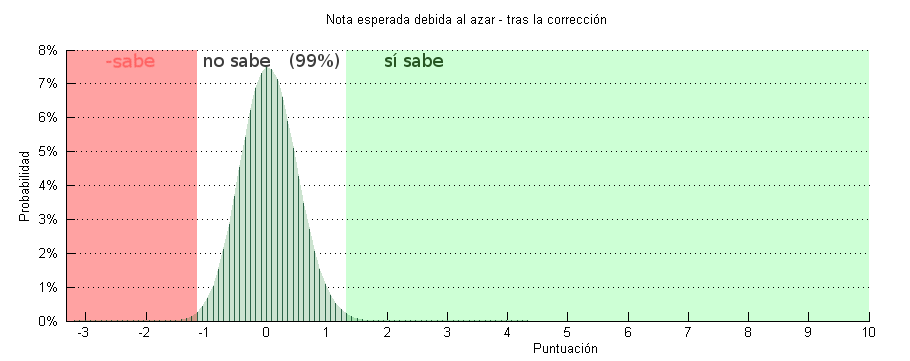
Esta es la gráfica completa de la que hemos visto antes, empieza en el -3.3 que es la nota más baja posible en un test de 4 opciones, y termina en el 10 que es la más alta.
Vamos a dividir el gráfico en tres regiones.
- La más grande y obvia es la región “no sabe”, alrededor del cero.
- Si nos movemos hacia la derecha, la región del “sabe”.
- Mientras que a la izquierda queda una región que, para alcanzarla hay que fallar adrede como decíamos antes, o bien tener los conceptos cambiados. Es el “menos sabe”.
Quiero calcular la nota que habría que sacar para asegurar con un 99% de posibilidades, que el examinado no lo ha hecho al azar. Se trata de un test de hipótesis de dos colas. En que la hipótesis nula es la nota se debe al azar y la hipótesis alternativa es esa nota no es por casualidad .
>> binoinv(0.01/2,150,0.25)*a+b
ans =
-1.1510
>> binoinv(1-0.01/2,150,0.25)*a+b
ans =
1.3270
Luego hay una posibilidad entre 200 (0.5%) de sacar una nota por debajo del -1.15 por azar, y la misma de sacar más de un 1.33. Mientras que el resto -el 99%- de que esté contenida entre ese rango. Coloreamos las regiones en el gráfico siguiente. Si cae dentro de la región blanca, no descartamos la hipótesis nula, así que la nota puede deberse al azar o no. Simplemente no tenemos datos para afirmar nada.
Lo que está claro es que, una vez compensado el azar, quien saca un 3 es porque sabe; no lo suficiente, tal vez, pero no ha respondido lo primero que se le pasa por la cabeza. Mientras que quien saca un -2 es que también sabe; sólo que al revés. O ha fallado a propósito o tiene confundidos los conceptos.
Todo esto lo averiguamos a través de la estadística porque el examen constaba de 150 preguntas, que son muchas. No siempre la distribución es tan estrecha, a medida que el examen tiene menos preguntas, esta se ensancha, y es más difícil aseverar nada.
Significación estadística
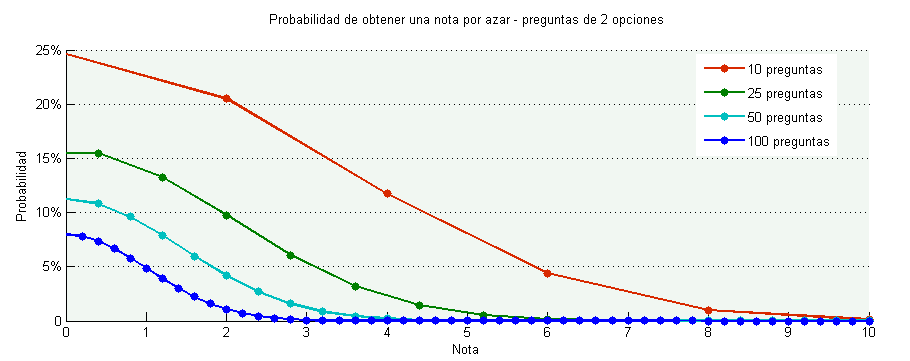
Como hemos dicho antes la fiabilidad del test depende del número de preguntas. En un examen de una pregunta, con dos opciones, tenemos un 50% de posibilidades de sacar un 10 y otro tanto de sacar un 0. Ahora ya me contaréis si ese resultado demuestra algo o no.
La probabilidad de que alguien apruebe de chiripa en un test de 150 preguntas con 4 opciones, la calculamos así:
>> 1-binocdf((5-b)/a,150,0.25)
ans =
0
Fijaos que he corregido la nota de 5 de acuerdo a los parámetros a y b que sacamos antes. Lo que calculamos ahí es la probabilidad de acertar 94 preguntas o más. 94 son las preguntas que se necesitan para un 5 (ver gráfico comparativo en la sección anterior). Es fácil de justificar: 150 preguntas, acertaríamos al azar 37.5 (un 25%), nos quedan 112.5. La mitad de 112.5 son 56.25. Y ahora 56.25 más las 37.5 dan 93.75. O sea las 94 que decíamos.
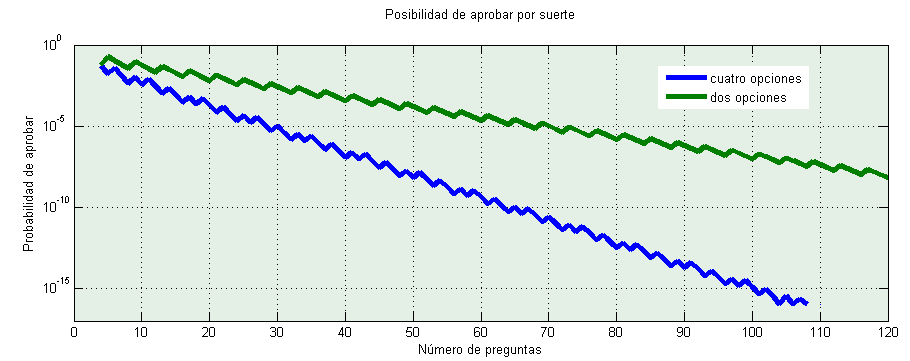
Por tanto probabilidad de aprobar por suerte un examen de 150 preguntas es prácticamente nula. Pero varía en función del número de preguntas. Según esta fórmula, donde n es el número de preguntas y p la probabilidad de acierto (la inversa del número de opciones, si son equiprobables):
n = 150
p = 0.25
( 1-binocdf((n-p*n)/2 + p*n, n, p) )* 100
Atención que la escala es logarítmica. Tiene lógica, mientras más preguntas y de más opciones más difícil que suene la flauta. Los escalones se deben a los decimales, es imposible aprobar una pregunta y media, y la distribución binomial es discreta. Pero al hacer la división salen decimales y no lo tenemos en cuenta. A pesar de eso la tendencia se aprecia claramente.
Y las posibilidades de obtener un 5, como decíamos antes, se desvanecen cuando aumenta el número de preguntas, pero son demasiado altas sobre todo en los test con pocas preguntas.
# Numero de preguntas y de opciones
n = 10;
o = 2;
# Probabilidad de acierto
p = 1/o;
# Parametros a y b de escalado
a = 10 / (n*(1-p));
b = 10 * (p/(p-1));
# Vector de preguntas
x = [0:n];
# Representación corregida
plot(a*x+b, binopdf(x,n,p))
Para terminar
Me doy por satisfecho si con este artículo he conseguido transmitir tres simples cosas:
- Hacer que cada pregunta fallada reste una cantidad es matemáticamente idéntico que exigir más del 50% para aprobar y es absolutamente necesario hacer alguna de las dos cosas. Sin embargo no hay que aplicar los dos métodos anteriores al mismo tiempo, a menos que sepamos que muchas preguntas son conocidas y queramos subir explícitamente el nivel.
- Si optamos por la resta, cada pregunta debe restar una fracción de punto equivalente a la inversa del número de opciones menos una.
- Hay un límite mínimo de preguntas para que un examen sea fiable: un examen de 5 preguntas con dos opciones no demuestra nada.
Todo lo anterior referido a exámenes de una sola opción correcta en la que todas las opciones son a priori igualmente probables. Luego habrá preguntas trampa, como las preguntas de elección múltiple que ya son otro cantar, o las opciones que son todas verdades pero unas más verdaderas que otras. Lo cual me recuerda este comentario que leí hace un tiempo en meneame.
Me acuerdo de un profesor al que le dije en una revisión “eso es como si me preguntas ‘Ronaldo es a) brasileño b) futbolista c) jugador del Madrid d) rico’ y el tío fue y me dice ‘claramente es la a, porque Ronaldo dentro de X años estará retirado y puede que no tenga tanto dinero como ahora pero no podrá evitar haber nacido en Brasil’